不收藏會后悔系列 | 談一談坐標轉換之七參數坐標轉換永遠是測繪工作離不開的一個話題。坐標轉換的方法很多,有的方法可以用相應的參數來描述,其中使用較廣的一個是七參數。七參數大多用于不同坐標系統間的基準變換。 七參數的由來 對于非測繪的專業人士可能不太能理解“基準”這個詞語。簡單的理解就是坐標數值的零點,比如空間坐標的原點,再比如大地坐標的起算面。定義一個坐標系的三個基本要素是原點、指向、尺度。原點即坐標系的原點,指向即坐標軸的指向,尺度即長度單位和橢球。由于各個坐標系,或者說定義坐標系的組織所確定的這三個要素都有所區別,這就產生基準的變換,并且使用七參數在空間坐標中進行基準變換。 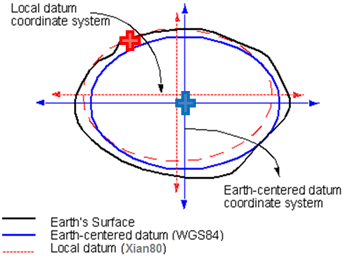 什么是七參數,又有哪七個參數呢? 七參數主要分為3類參數,旋轉、縮放和平移。縮放,表示為k,主要是由于測量誤差產生的;平移為3個坐標軸方向上的平移,表示為dX、dY、dZ,這是由于原點不一樣產生的;旋轉為3個坐標軸的旋轉,表示為rX、rY、rZ,這是坐標軸指向不一致產生的。關注并星標《測繪之家》微信公眾號,獲取更多測繪技術干貨。 值得注意的是,旋轉存在方向的問題,不同的軟件,或者說不同地域的人的習慣差異,致使旋轉方向不一致,比如南方集團與天寶七參數旋轉方向一致,但與ArcGIS的就相反。因此同一個七參數在不同軟件中使用時需要考慮旋轉方向的問題,適當的時候做相應的變換才能完成正確的坐標轉換,即旋轉方向定義相反時,旋轉角取其相反數。 平移的單位為對應的長度單位,我們常用米;旋轉的單位為秒,原因是各個坐標系間指向的差異都很小;縮放的單位是PPM(part(s) per million,百萬分之一),也就是說縮放是一個特別小的數值,這是因為坐標轉換前我們都會率先統一單位,所以縮放數值也就體現了測量誤差等因素的影響。
七參數的應用 參數的應用過程細分為旋轉、縮放、平移三個過程。這三個過程的順序是如何的,我們來看一下公式: 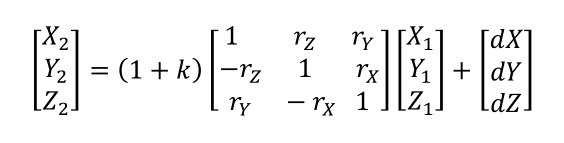 簡化為: 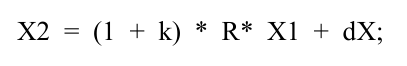 上式中,X1為原始空間坐標,X2為目標空間坐標,K為縮放,R為旋轉,dX為平移。 可以看出,該順序是先旋轉,再縮放,然后平移。當然與之相反的是先平移,再縮放,然后旋轉,這是一個可逆的過程,方便了兩個空間坐標來回的轉換。這里為了方便說明,我們將旋轉、縮放、平移定義為七參數的正應用;平移、縮放、旋轉定義為七參數的反應用。關注并星標《測繪之家》微信公眾號,獲取更多測繪技術干貨。 我們可以看看EPSG對一個坐標系定義: +proj=longlat+ellps=krass+towgs84=28,-121,-77,0,0,0,0 其中七參數作為基準的定義,叫做towgs84,字面理解是轉換到wgs84所需的七參數,作用同樣是為了不同坐標系間的基準變換。EPSG在進行基準轉換前需要說明原始的towgs84和目標的towgs84兩個七參數。 那么問題來了! 兩個七參怎么進行基準變換呢?為什么和WGS84有關系呢?在對比我們的熟悉的工程之星和SGO的坐標轉換,通常都只有使用一個七參的情況,這又如何理解呢? 首先,工程之星和SGO大多的轉換場景都是WGS84坐標轉換到XIAN80、Beijing54、CGCS2000等坐標,這里使用的七參數是原始坐標系直接到目標坐標系的七參數;而EPSG定義的七參數(基準)是坐標系本身轉換到WGS84坐標的七參數,只要兩個坐標系都知道如何轉換到WGS84坐標,其實就間接的知道這兩個坐標系間的基準變換。 至于為什么是WGS84,這是歷史原因造成的。因為WGS84是最先建立起來的全球坐標系統,衛星定位大多得到的是WGS84的空間或者大地坐標,為了能轉換為自己的定義坐標系下的坐標,都需要自身建立與WGS84的關系。 下一問題,EPSG如何用兩個七參數進行基準變換。回到之前七參數的正反應用問題,原始坐標系的towgs84將原始坐標轉換為WGS84的坐標(以下簡稱84坐標),這里是正應用。得到84坐標后使用目標坐標系的towgs84得到最終的坐標,這里是反應用。其實我們的工程之星和SGO坐標轉換的原始坐標系和目標坐標系都可以指定七參數,只是使用的頻率較低常被我們忽略。但與前述的過程相反,原始坐標系的七參數是反應用,目標坐標系的七參數是正應用。隨著我們南方的發展壯大以及與國際的進一步接軌,使用兩個七參數進行基準變換的場景會越來越多,比如我們的新軟件GIStar,我們需要好好的理解其原理和過程,同時清楚現有功能和新功能的差異,使坐標轉換更加得心應手。 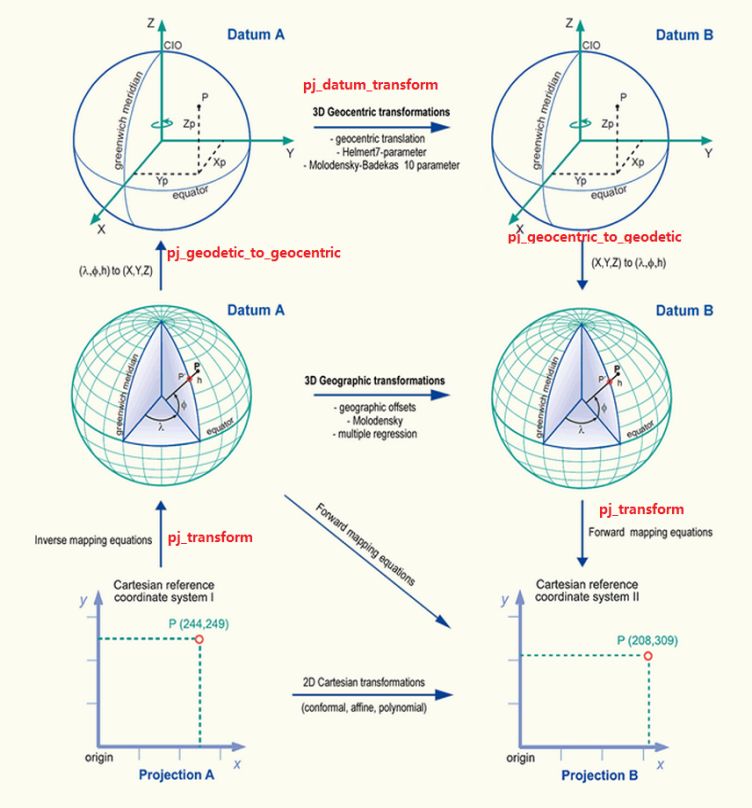 七參數的細節 與towgs84相反的是fromwgs84,在旋轉和縮放很小的前提下,兩者互為相反數。fromwgs84可以參考天寶的坐標轉換工具。如何區別towgs84和fromwgs84呢,其實很好理解,七參數正應用使非84坐標轉換為84坐標,那么該七參數為towgs84;七參數正應用使84坐標轉換為非84坐標,那么該參數為fromwgs84。我們工程之星和SGO以wgs84為原坐標系的轉換場景,其使用的七參數都為fromwgs84。關注并星標《測繪之家》微信公眾號,獲取更多測繪技術干貨。 回到前面提到的公式,該場景下X1為84坐標,X2為非84坐標,例如XIAN80,那么k、R和dX組成的七參數為fromwgs84,X2與X1調換,則為towgs84。 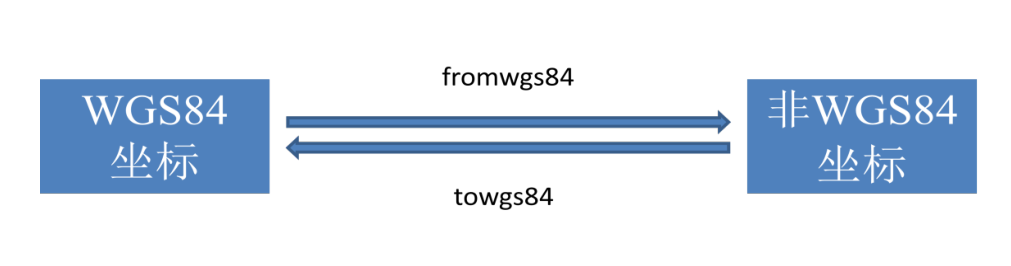 七參數的求解 求解7個參數,我們至少需要7個方程,一對空間坐標可以列3個方程,也就是說我們需要至少3對點,通過最小二乘的方法解算出七參數。當然點的數量也是有講究,不是剛好3個點就好,也不是點越多越好,具體需要參考實際情況。 七參數作為基準變換的工具,其適用較大的區域乃至全球,我們需要在該區域選擇均勻分布的控制點來求解七參數。小區域所求解的七參數是不適用的。這里再提一下towgs84和fromwgs84,原為非84坐標,目標為84坐標,所求得的七參數為fromwgs84,相反則為towgs84。 以上為坐標轉換七參數的介紹,希望對大家有所幫助。 來源:科力達儀器 本文限于行業學習交流之用,版權、著作權歸原載平臺及作者所有。我們尊重作者的成果,如涉嫌侵權,請聯系我們及時刪除。 |
||||||||||||||||||||||||